Axiomatic Attribution for Deep Networks (feat. Integrated Gradient)
Paper: Axiomatic Attribution for Deep Networks (https://arxiv.org/abs/1703.01365)
논문 요약보다는 내가 이 논문을 어떤 방향으로 이해했는지, 그리고 실제로 적용하면서 중요했던 것이 무엇이었는지 적었다.
핵심 아이디어
방향성
기본적으로 이 논문은 신경망의 결과물을 Scalar Function으로 보고, 신경망의 Gradient를 Conservative Vector Field로 생각한다. 그리고 이를 통해 신경망의 예측값을 수식적으로 어떻게 표현할 수 있는지 파악하여 XAI로 활용한 것에 불과하다.
즉, 논문 전체의 아이디어는 하나의 수식이고, 나머지는 이 수식을 정당화하기 위한 문제 제기, 그리고 검증의 과정이다. 수식 자체도 굉장히 단순하며, 쉽게 구현할 수 있는 수식이다.
목표
n차원의 feature vector X=(x1, x2, … xn)이 있고, 이를 input으로 받는 신경망 F가 있다고 하자. 우리는 신경망의 output인 F(X)에 대한 xi의 기여도를 알고싶다. 즉, F(X) = sum(G(xi))인 어떤 함수 G를 찾고 싶다.
접근 방식
F(X)를 sum(G(xi)) 형식으로 유도해보자.
- 일단 신경망 F는 scalar funtion으로 생각할 수 있다.
- 따라서, ∇F는 conservative vector field다. 즉, ∇F에 대한 경로 적분은 Path Independent이다.
- ∇F에 대한 경로 적분은 경로와 상관 없이 F(path end) - F(path start)라는 이야기다.
- 경로와 상관 없이 Energy는 Path Independent 한 것과 같다.
- 경로를 아무렇게나 잡아도 적분값은 똑같으니까, 가장 간단한 경로인 Straight Path를 잡자. (질문 1로 이어짐)
- 그럼 아래와 같이 계산할 수 있다.
고민했던 것들
왜 굳이 straight path로 잡나?
사실 이론적으로는 어떤 경로를 잡던 상관이 없다. 어차피 ΔF = F(path end) - F(path start)이기 때문이다. 처음에는 fluctuation error를 최대한 피하려고 최단거리인 straight path를 잡지 않았나 싶었는데, 어차피 신경망 안쪽의 gradient가 나타내는 vector field가 어떤 모양인지를 모르니 별로 상관이 없다.
근데 경로를 이상하게 잡으면 저렇게 깔끔하고 간단한 수식으로 Integrated Gradient를 표시할 수가 없잖아? 그러니까 경로가 상관이 없으면 그냥 간단한 수식으로 쓰자.
내가 계산한게 제대로된 값인지는 어떻게 아나?
우리는 continuous한 Integral을 계산할 수 없으니 근사적으로 discrete summation을 계산하는데, 이때 approximation 에러가 발생한다. Integrated Gradient에서 발생하는 에러는 크게 두 가지로, (1) ∇F의 fluctuation에서 발생하는 에러와 (2) Step 수가 충분히 크기 않아서 발생하는 에러가 있다.
에러가 얼마나 되는지 확인하려면 ΔF = ∑IG(xi)를 계산해본다. 좌항은 신경망에서 얻을 수 있는 정확한 값으로, F(path end = input) - F(path start = baseline)로 계산한다. 우항은 모든 feature element의 Integrated Gradient를 합한 것이다. 이론적으로 좌항과 우항은 같아야 한다. 따라서 우항이 좌항에 얼마나 가까운지 계산하면 discrete summation에서 발생한 에러율을 알 수 있다.
실제 상황에서 Integrated Gradient가 제대로 계산되었는지 확인하는 것은 매우 중요하다. baseline을 잘못 잡거나, step수가 충분치 않아 IG를 완전히 잘못 계산하는 경우가 많다. 그러니까 꼭 좌항과 우항이 비슷한지 확인해보고, 너무 차이가 난다면 baseline을 잘 잡거나 step 수를 늘려서 에러를 줄이자.
어떤게 좋은 baseline인가?
좋은 baseline을 잡으면 computing resource를 줄일 수 있다. 적은 step 수로도 정확한 값을 얻을 수 있기 때문이다. (경험상 baseline을 잘 잡으면 step 수를 1/10 수준으로만 사용해도 된다. 즉, computing resource를 90% 감소시킬 수 있다.)
반대로 말하면, 거지같은 baseline을 잡아도 step수만 충분하면 정확한 IG 값을 얻을 수 있다는 뜻이긴 하다. 하지만 신경망이 무거우면 step수를 늘리는 것도 부담이므로, 왠만하면 baseline을 잘 선택하자.
좋은 baseline은 neutral한 baseline이면서, computing resource를 최소화하는 것이다. 아래는 내가 사용하면서 좋았던 것들이다:
- zero vector 사용하기 (논문에서도 대표적인 neutral baseline으로 zero vector를 소개했다.)
- embedding layer가 있다면, embedding space의 zero vector 사용하기. 그러니까 text encoding 단계의 index를 그대로 사용하지 말라는 뜻이다. 이러면 인접한 index의 token들 때문에 불필요한 fluctuation이 너무 많이 발생한다. )
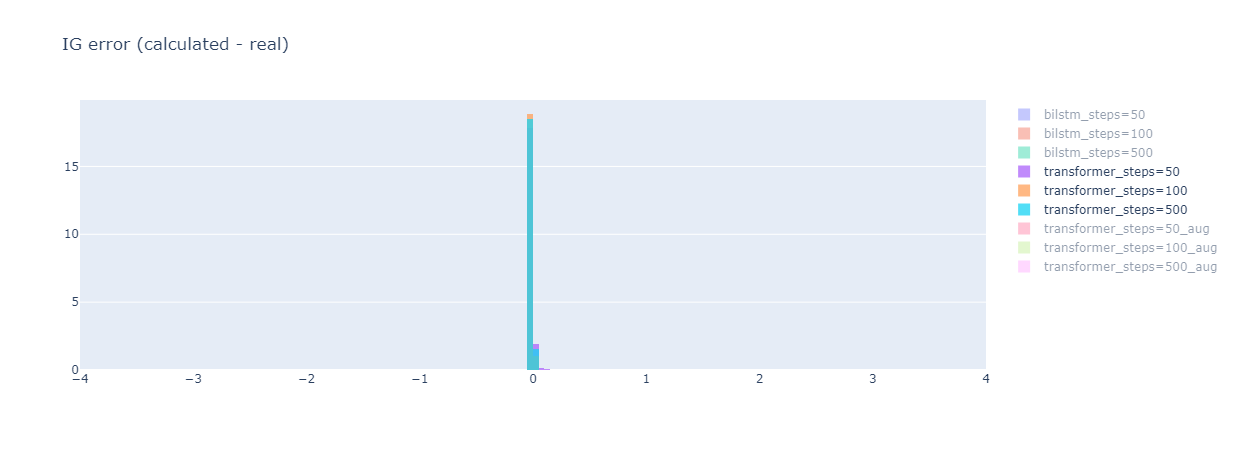
실제로 encoding 단계에서 zero vector를 사용하는 것보다 embedding space에서 zero vector를 사용하는게 에러율이 훨씬 작다. 정말 훠어어어얼씬 작다.
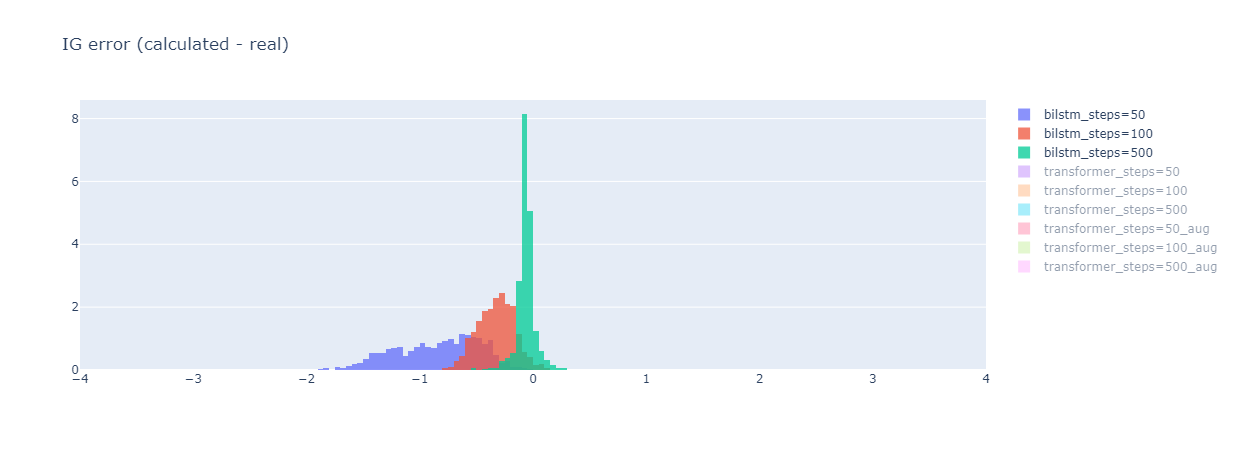
아래는 회사에서 사용한 모델이다. 눈여겨 볼 점은:
- Steps 수를 늘리면 데이터들의 Integrated Gradient Error (IG Error) 분포가 뾰족해진다.
- 즉 RMSE가 작아진다.
- Steps=50에서 IG Error가 얼마나 큰지 보라. 지금 모델이 Binary Classification 모델인데, IG Error가 -1이 넘는 것들이 엄청나게 많다.
- Bilstm 모델은 Encoding 단계에서 zero vector를 사용했고, Transformer 모델은 Embedding 단계에서 zero vector를 사용했다. (모델 차이도 있겠지만) 어느 단계에서 zero vector를 사용하는지에 따라서 IG Error 분포는 확연하게 다르다.