Abnormal Detection Using Noised Binomial Distribution with CLT
1. Introduction
1-1. 배경
IP 기반의 Abnormal Detection 모델을 좀 더 정교하게 다듬을 일이 생겼다. 목표는 다음과 같이 크게 두 가지이다:
- 목표 1: 어떤 방식으로든 Threshold가 하드코딩된 값이 아니라 Daily로 계산되어서 Data Shift를 잘 반영해야 한다는 것
- 목표 2: VPN 사용으로 IP가 오염되었을 때, 오염된 IP와 오염되지 않은 IP를 구분할 수 있어야 한다는 것
1-2. 방향성
이를 위해 현재 상황을 수학적으로 모델링하고, Daily Data Shift를 적용할 수 있는 모델로 개선한다. 사실 지금 모델은 Rule Based Model과 다를 바 없으니, 이를 개선하는 것을 목표로 한다. 이 과정을 수식화하고 정리해두면 나중에 다시 써먹을 일이 있을 것 같아서 여기에 정리해놓는다.
1-3. 기타 사항
- 기타 1: 궁극적으로는 설명 가능한 ML 모델, 즉 XAI가 가미된 ML-based Abnormal Detection 모델을 만드는 것을 목표로 한다.
- 기타 2: 실무에서는 ML적인 접근 말고도 기획적으로 해결할 수 있는 부분들도 많이 있더라. 이러면 적은 노력으로 큰 효과를 얻을 수도 있다.
2. Theory
2-1. 문제 정의
IP가 오염된 경우를 아래와 같은 Noised Binomial Distribution으로 생각한다:
- 정상적인 경우: 모든 IP는 같은 분포에서 샘플링하여 만들어진 표본집단이다. 따라서 같은 success probability를 공유하지만, 각 집단의 크기는 다르다. (어떤 행동을 success로 정할지는 실제로 풀고자 하는 경우에 따라 다르다.)
- 비정상적인 경우: 누군가 악의적으로 정상적인 IP에 success noise를 대량으로 주입한다.
내게 주어진 정보는 아래와 같다:
- 정보 1: 어떤 IP가 정상인지 비정상인지는 모르지만, 각 IP가 가진 표본 집단의 크기와 각각의 success rate은 알고 있다.
- 정보 2: 이러한 IP의 정보를 N개 알고있다.
여기서 내가 알아내고자 하는 건:
- 어떤 IP가 정상인지 비정상인지 구분하는 것이다.
2-2. 모델링
아래와 같은 순서로 문제를 접근한다:
- 단계 1: 정상적인 데이터 분포의 Binomial success probability
p를 추정하기 - 단계 2: 표본 집단의 Binomial success probability 추정값
p가 정상적으로 발생할 확률 구하기
표본집단의 success case 수를 Z라는 Variable로 표현하자. 만약 i번째 표본집단이 정상적인 경우라면 success case를 아래와 같이 표현할 수 있다:
만약 i번째 표본집단이 비정상적인 경우여서 success case에 ε 만큼의 노이즈가 섞인다면 아래와 같이 표현할 수 있다:
만약 비정상적인 경우가 발생할 확률을 π라고 한다면, 일반적인 success case 수를 아래와 같은 Mixture Distribution으로 표현할 수 있다:
이는 아래와 같이 간략하게 표현할 수도 있다:
\[X \sim B(n, p)\] \[Y \sim Bern(\pi) \\ N \sim g(\theta)\] \[Z \sim X \ + Y \cdot N\]이 경우, 해당 표본집단의 success probability 추정값의 기대값과 분산은 아래와 같다:
\[\begin{align} E[\hat{p}] &= E \left[ \frac{Z}{n} \right] = \frac{1}{n} E[Z] \\ &= \frac{1}{n} \left( E[X] + E[Y] \cdot E[N] \right) = \frac{1}{n} \left( np + \pi \cdot E[N] \right) = p \ + \ \frac{\pi \cdot E[N]}{n} \end{align}\] \[\begin{align} Var(\hat{p}) &= Var \left( \frac{Z}{n} \right) = \frac{1}{n^2} Var(Z) \\ &= \frac{1}{n^2} \left( Var(X) + Var(YN) + 2 \cdot Cov(X, YN) \right) \\ &= \frac{1}{n^2} \left( Var(X) + Var(YN) \right) \\ &= \frac{1}{n^2} \left( np(1-p) + E[Y^2] \cdot E[N^2] - (E[Y] \cdot E[N])^2 \right) \\ &= \frac{1}{n^2} \left( np(1-p) + \pi \cdot E[N^2] - \pi^2 \cdot (E[N])^2 \right) \\ &= \frac{1}{n^2} \left( np(1-p) + \pi \cdot (Var(N) + (E[N])^2) - \pi^2 \cdot (E[N])^2 \right) \\ &= \frac{p(1-p)}{n} + \frac{\pi \cdot Var(N) + \pi(1-\pi) \cdot (E[N])^2}{n} \end{align}\]기대값과 분산의 각 항에 주목하자. Mixture Distribution을 쓸 때부터 자명한 결과지만, 기대값과 분산의 첫 항은 정상적인 표본집단이 모여서 만드는 분포이며, 나머지 항들은 비정상적인 표본집단의 노이즈로 인해 success probability가 정상보다 크게 왜곡되어 나타난 결과이다.
즉, 모든 표본집단의 success probability를 구하고 histogram을 그려보면, one peak distribution를 베이스로 노이즈가 섞인 결과를 볼 수 있음을 예상할 수 있다. 이를 실제 실험으로 확인해보자.
3. Experiment
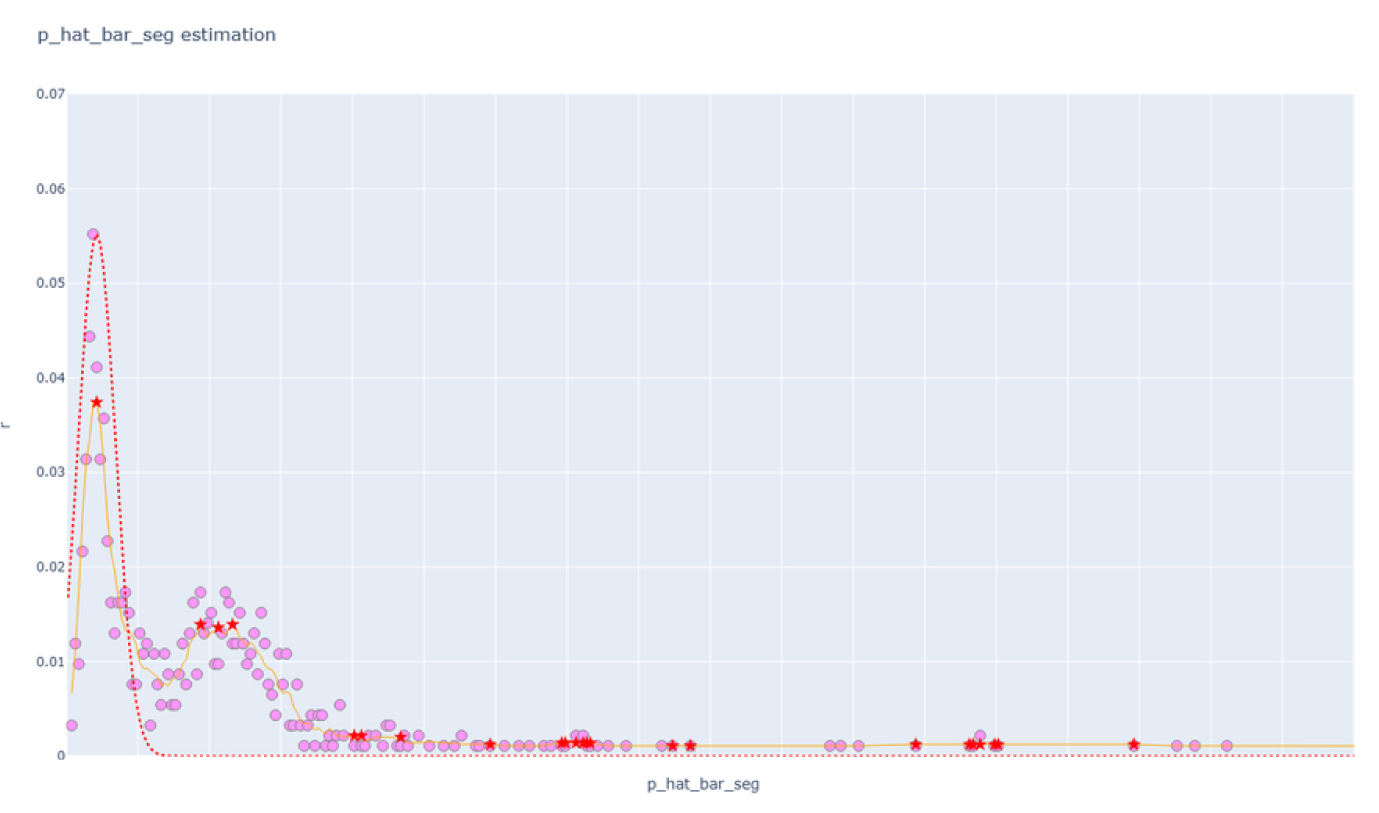
분홍색 점은 실제 데이터의 히스토그램 값, 주황색 선은 히스토그램 값의 smoothing line, 빨간색 선은 Theory 파트의 수식으로 계산한 예측 분포이다. 여기서 주목할 점은 아래와 같이 크게 2가지이다:
- 주목 1: 이론에서 예측한 바와 같이, 정상적인 success probability는 분포 상에서 하나의 Peak로 나타난다.
- 이 분포는 이론에서 예측한 기대값과 분산을 거의 정확하게 따르고 있음을 알 수 있다.
- 주목 2: 이론에서 예측한 바와 같이, 비정상적인 success probability는 분포 상에서 정상적인 success probability보다 큰 분포로 나타난다.
- 여기서 비정상적인 success probability 또한 완전히 랜덤한 노이즈가 가해지지는 않은 것으로 보여, 좀 더 넓은 분산을 가진 두 번째 피크로 나타남을 알 수 있다.
4. Conclusion
이제 정상적인 success probability를 알아냈으니, 어떤 표본집단이 주어진 경우 해당 표본집단의 success probability가 우연히 발생할 확률을 구할 수 있다. 이는 단순히 Binomial Distribution의 CDF이므로 자세한 설명은 생략한다.
실무에서 사용할 때는 좀 더 유의해야 할 점들이 있다:
- 유의점 1: 위와 같이 정상적인 분포와 비정상적인 분포가 해상도 내에서 구별 가능할 정도로 나타나는 것은 매우 운이 좋은 경우다. 만약 매우 작은 노이즈가 빈번하게 끼는 경우, 해상도 내에서 유의미하게 두 분포를 구분하지 못할 수도 있다.
- 유의점 2: 이를 가지고 Daily Data Shift에 대응하기 위해 유동적인 Threshold를 구하는 작업은 각 실무의 성격에 맞게 튜닝해야한다. 특히 Peak를 찾는 알고리즘에 많은 신경을 기울여야한다.